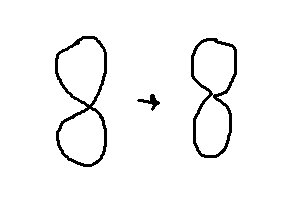Ein besonders spannender Typ von offenen Fragen sind Grafik-Fragen und dabei besonders die Variante, bei der auf einem Bild etwas markiert werden muss, da sich hier der Überdeckungsgrad der Markierung der Lernerin mit der von der Autorin festgelegten Region automatisch berechnen und das Ergebnis sich auch gut visuell erklären lässt.
Doch so ganz einfach ist das alles nicht ...
Eingabe
Das Zeichentool, das im CaseTrain-Player für das Markieren von Inhalten und für das Notizbuch verwendet wird (
sketch.js) wurde für die Grafik-Markierungs-Fragen so erweitert, dass es immer eine geschlossene Fläche erzeugt, in dem der aktuell letzte Punkt des Streckenzugs (Polygon) immer mit dem Startpunkt verbunden wird.
Das erste Problem dabei ist schonmal, dass die Lernerin auch ein sich selbst überschneidendes Polygon zeichnen kann, in dem dann auch Lücken enthalten sein könnten.
Komplexe Polygone in einfache Polygone umwandeln
In einfacheren Fällen wären das Polygone mit einer Überschneidung wie eine 8, die man auch einfach so interpretieren könnte, als wären sie nicht selbst überschneidend.
Man kann aber auch leicht solche Polygone erzeugen:
Das macht zwar keinen Sinn, aber Lernerinnen (und Lerner) machen sowas ... und je nach Polygon-Färbungsregel entsteht dann ungefähr so eine Fläche:
Damit könnte man theoretisch einfach weiterarbeiten (immerhin kann man damit Lücken malen, vielleicht soll das so sein), aber das wäre nicht sinnvoll, da beim Zeichnen schwer vorhersehbar ist, wo die Lücken entstehen werden.
Eine Möglichkeit, solche Formen zu vereinfachen ist, die konkave Hülle zu berechnen - dafür gibt es eine Javascript-Bibliothek (
concaveman @ github), der man einfach eine Menge der Punkte des Objekts übergibt und die dann die Punkte des Polygons für die konkave Hülle zurück liefert - aus Effizienzgründen muss man dabei das entstehende Polygon etwas vereinfachen, da sonst alle Punkte des Randes im Ergebnis-Polygon landen:
 |
| Eingabe |
 |
| Ausgabe mit überlagerter Hülle (mit transparentem Gelb gefüllt) |
Dieses Ersetzen der ursprünglichen Markierung durch die konkave Hülle darf aber nur geschehen, wenn sich das Polygon auch selbst schneidet. Falls die Lernerin absichtlich eine sich fast überschneidende Markierung eingibt, darf die Hüllung nicht angewendet werden, da diese wegen der Formvereinfachung die kleine Lücke schließen würde und der Ring durch ein komplett gefülltes Objekt ersetzt würde:
Man kann daher also nicht einfach die Hüllung immer verwenden, sondern nur wenn vorher festgestellt wurde, ob tatsächlich eine Selbstüberschneidung stattfindet oder nicht. Noch nicht gelöst ist dabei das Problem, wenn die Lernerin tatsächlich eine Donut-Form zeichnen will (ähnlich wie oben) aber absichtlich die Form (durch Überschneidung) schließt:
Ich habe noch keine Möglichkeit oder Heuristik gefunden, so eine absichtliche Selbstüberschneidung von einer versehentlichen, die es zu reparieren gilt, zu unterscheiden. Momentan wird daher jedes Polygon mit Selbstüberschneidung durch Hüllung repariert.
Um Selbstüberschneidungen zu finden vergleicht man "einfach" jedes Segment des Polygons mit jedem anderen und testet auf Überschneidung - dafür gibt es effiziente Algorithmen wie Bentley-Ottmann (
Wikipedia), die auch schon in Javascript implementiert wurden (
isect @ github). Ein Problem dieses Algorithmus' ist, dass sich zwei benachbarte Segmente
immer in ihrem Verbindungspunkt "schneiden", weshalb das Polygon erst mit passenden Lücken versehen werden muss. Dies könnte naiv passieren, indem man einfach jeden Endpunkt eines Segments um -1/-1 verschiebt - was aber wiederum dazu führt, dass andere falsche Überschneidungen passieren (etwa wenn das Polygon danach einen Knick macht und damit den neuen Endpunkt schneidet obwohl es den ursprünglichen Punkt nicht geschnitten hätte). Lücken führen nur dann zu keinen Problemen, wenn die Segmentstrecken verkürzt werden ohne dass ihre Richtung geändert wird - dazu werden die (kartesischen) Koordinaten des Endpunkts von jedem Segment in Polarkoordinaten umgewandelt (
Wikipedia), der Radius (und damit die Länge) wird um 1% verkleinert und die Koordinaten werden wieder ins kartesische System zurückübersetzt:
Da die Lücke damit immer zwischen zwei Pixeln liegt (kein Polygon hat Segmente die länger als 100 Pixel sind) können die Lücken nicht dazu führen, dass eine Überschneidung übersehen wird.
Praktischerweise bietet die verwendete Javascript-Bibliothek die Möglichkeit, die Überschneidungsberechnung beim Finden der ersten Überschneidung abzubrechen - da uns die Position der Überschneidungen bzw. überhaupt das Berechnen aller Überschneidungen nicht interessiert, ist die Berechnung damit wesentlich effizienter.
Mehrere Markierungen
Wie soll man damit umgehen, dass die Lernerinnen mit dem Zeichentool auch mehrere Markierungen setzen können? Verbieten ist schlecht, da das zum einen schwer zu kommunizieren ist - soll man das Zeichentool deaktivieren, wenn eine Markierung gesetzt ist und reaktivieren, wenn die Lernerinnen UNDO wählen? Soll man die erste Markierung kommentarlos durch die zweite ersetzen? Das wäre blöd, wenn sich die Lernerin bei der ersten Markierung viel Mühe gegeben hat und vielleicht mit der zweiten Markierung die erste nur ein bisschen verbessern wollte. Soll man jedesmal einen Hinweis einblenden, wenn der Markierungsbildschirm geöffnet wird oder soll irgendwo anders ein Hinweis hinterlegt sein, der durch Anklicken eines Icons geöffnet werden kann? Niemand liest Anleitungen ...
Aber da es den Autorinnen sowieso möglich sein soll, mehrere Regionen anzugeben, die zu markieren sind, sind diese Überlegungen eh müßig, denn dann müssen sowieso mehrere Markierungen möglich sein.
Bei mehreren Markierungen hat man dann wieder das Problem, dass man mit überlappenden Markierungen umgehen muss - es zu verbieten, dass sich Markierungen überlappen ist algorithmisch zwar möglich aber zu aufwändig (insbesondere auf unseren Prüfungs-iPads würde hier die Oberfläche unresponsiv werden). Mit überlappenden Markierungen einfach so weiterzuarbeiten ist aber auch nicht sinnvoll, da dann Regionen mehrfach überdeckt wären oder - für die Bewertung schlimmer - Pixel außerhalb von Regionen mehrfach überdeckt wären und zu doppeltem Abzug führen würden. Markierungen die sich überlappen müssen also vereinigt werden, schon allein deshalb weil die Lernerin eine gesetzte Markierung vielleicht erweitern will und dann mit zwei einander berührenden Markierungen weiterzuarbeiten, ist vielleicht auch nicht sinnvoll.
Mit den bisher eingesetzten Mitteln wäre das vielleicht einfach lösbar: Jede Markierung mit jeder anderen auf Überlappung testen (Markierung 1 malen, Pixel zählen, Markierung 2 transparent malen, Pixel zählen, bei Differenz überlappen sich die beiden), danach die Markierungen malen, alle Pixel bestimmen, konkave Hülle, fertig.
Jedoch, es wird komplizierter - denn Lernerinnen können z.B. mit mehreren Markierungen auch folgendes erzeugen:
 |
| links: erste Markierung, rechts: erste Markierung + weitere Markierung |
Hier würde die konkave Hülle nach Eingabe der zweiten Markierungen den gesamten Innenraum mit ausfüllen und das wäre im Beispiel offensichtlich nicht beabsichtigt. Ab hier kann also nicht mehr mit komplett gefüllten Polygonen gearbeitet werden, sondern man muss mit Polygonen arbeiten, die beliebig viele Löcher (innenliegende Polygone) haben können. Mehrere Löcher könnten z.B. entstehen, wenn weitere überlappende Markierungen eingegeben werden:
Hier kann man sich natürlich die Frage stellen, ob man
dafür wirklich einen Mechanismus vorsehen muss - aber wer weiß schon, welche Fragen sich die Autorinnen noch ausdenken werden? Und was die Lernerinnen dazu markieren werden? Zum Glück gibt es für das Vereinigen von Polygonen eine effiziente Javascript-Bibliothek, bei der es auch noch egal ist, ob das Polygon eine oder beliebig viele Löcher hat (
Javascript Clipper @ SourceForge). Damit ist das Überlappen gelöst.
Und somit ist die Eingabe der Markierungen fast erledigt: Jede Markierung wird auf Selbstüberschneidung geprüft und ggf. durch die konkave Hülle ersetzt. Anschließend wird jede Markierung mit jeder anderen auf Überlappung getestet und sich überlappende Markierungen durch ein Polygon (mit ggf. Löchern) ersetzt, diese beliebig löchrigen Polygone werden wiederum miteinander verglichen usw. bis man am Ende separate Markierungen hat.
Ein kleines Problem ist hier nur die Geschwindigkeit:
Das Pixelzählen (zur Entdeckung der Überlappung) kostet Zeit und die Überprüfung auf Selbstüberschneidung kostet ebenso Zeit. Auf einem iPad ist das solange nicht spürbar, wie es nur wenige Markierungen gibt - aber wenn es viele kleine sich überschneidende Markierungen gibt, würde die Bedienung dann träge, wenn bei jeder neu hinzukommenden Markierung die entstehenden Polygone komplett neu berechnet werden. Daher werden zu jeder Markierung die daraus resultierenden Polygone gespeichert und bei einer neu hinzukommenden Markierung muss nur noch diese eine Markierung ggf. repariert werden und danach nur mit den gespeicherten Polygonen verglichen werden. Bei UNDO kann der vorherige Zustand sofort ohne Berechnung wiederhergestellt werden.
Eine weitere Optimierung, die angewendet wird, ist die Beschränkung beim Pixelzählen auf die relevanten Bereiche: Beim Pixelzählen zur Bestimmung der Überlappung zweier Polygone wird zuerst das umgebende Rechteck um jedes Polygon berechnet. Danach kann schnell berechnet werden, ob diese beiden Rechtecke überhaupt überlappen, und nur falls das möglich ist, werden die Polygone überhaupt gemalt. Und dann werden auch nur die Pixel gezählt, die sich im Rechteck befinden, das die beiden Rechtecke der gerade zu vergleichenden Polygone umgibt.
Ebenso wird beim Bilden der konkaven Hülle der Algorithmus nur auf das Rechteck angewendet, das das zu reparierende Polygon einschließt.
Technologie-Demo der Eingabe (Markierungen sind rot mit dünnem schwarzen Rand, Ergebnis-Polygone werden mit grünem Rand und transparent gelber Füllung darüber gemalt)
Auswertung
Bei einer idealen Bewertungsvorschrift gäbe es für jedes Pixel im Bild eine Wert, wie richtig oder falsch dieses Pixel ist, am Ende zählt man den Wert aller markierten Pixel zusammen und verrechnet das noch mit den nicht überdeckten Bereichen jeder Region.
Eine gute Vorschrift um den Korrektheitswert eines Pixel könnte sein, dass Pixel, die "nahe" an der Region sind, weniger falsch sind als Pixel, die weit entfernt sind - also etwa so:
 |
| Der grüne Kreis in der Mitte stellt eine einfache Region dar. |
Wenn mehrere Regionen mit anderen Charakteristika existieren, dann wäre das Feld etwas komplizierter:
Im Prinzip könnte man jetzt einfach jedem Pixel die Bewertung geben, die sich aus obigem Bild ergibt, grün wäre richtig, rot wäre ganz falsch, die Farben dazwischen geben die jeweilige Falschheit an. Aber was passiert dann hier?

Sollte hier der Punkt A wirklich genauso falsch sein, wie die Punkt in der Ecke ganz oben rechts? Sollte er doppelt falsch sein, weil er außerhalb beider Regionen liegt? Oder sollte er weniger falsch sein, weil er insgesamt näher an beiden Regionen liegt? Und was ist mit Punkt B, falls die Lernerin die eingezeichnete Markierung gemacht hat? Sollte er wirklich als Überdeckung zur Region links oben und damit positiv zählen oder sollte er als rot gelten, da die Lernerin offensichtlich die Region rechts unten markieren wollte und den Bereich um B zu viel markiert hat? Hier stößt eine automatische Auswertung an ihre Grenzen - wobei sich vermutlich auch leicht Beispiele konstruieren ließen, bei denen sich eine menschliche Korrektorin auch schwer tun würde und die Lernerin fragen müsste, was sie gemeint hatte.
Zudem wurde zu den drei letzten Bildern noch gar nicht erwähnt, wie man überhaupt auf die Breite der Übergangsbereiche oder den genauen Verlauf des Falschheitswertes innerhalb des jeweiligen Übergangsbereichs kommt? Es ist ja vorstellbar, dass auf der einen Seite einer Region der Übergang relativ kurz und scharf sein müsste, aber auf der anderen Seite es auf etwas weniger oder mehr gar nicht wirklich ankommt. Die genauen Charakteristika müsste auf jeden Fall die Autorin eingeben - und da das mit vertretbaren Aufwand gar nicht praktisch möglich ist, kann die Bewertung hier leider auch nicht (falls das überhaupt technisch möglich wäre) optimal fair stattfinden.
Deshalb wird die Bewertung hier so vereinfacht, dass alle Punkte außerhalb der Region gleich falsch sind. Bei der Berechnung der Überdeckung einer Region mit einer Markierung ergeben sich somit 4 Arten von Pixel: Solche die in der Region und der Markierung liegen, solche die in der Region und außerhalb der Markierung liegen, solche die außerhalb der Region und innerhalb der Markierung liegen und solche die außerhalb der Region und außerhalb der Markierung liegen.
Um diese miteinander zu verrechnen, erhält jede Region die Werte m1 und m2:
* Wie viele Minuspunkte zählt ein nicht-markiertes Pixel der Region (Minuspixel Typ 1) (m1)
* Wie viele Minuspunkte zählt ein zuviel markiertes Pixel außerhalb der Region (Minuspixel Typ 2) (m2)
* Jedes Pixel innerhalb von Region und Markierung zählt +1 (Pluspixel)
Die Bewertung ist dann:
(Anzahl Pluspixel - m1 * (Anzahl Minuspixel Typ 1) - m2 * (Anzahl Minuspixel Typ 2)) / (Anzahl Pluspixel + Anzahl Minuspixel Typ 1)
Da es praktisch unmöglich ist, eine Region exakt zu markieren, gibt es zusätzlich noch einen Schwellwert, ab dessen Erreichen 100% gegeben werden. Zusätzlich erhält jede Region noch ein Gewicht für die Gesamtbewertung. Und damit ist der Überdeckungsgrad einer (oder mehrerer) Markierungen mit einer Region recht einfach zu berechnen.
Wie berechnet sich aber der Überdeckungsgrad, wenn eine Markierung mehrere Regionen überdeckt und diese Regionen ihre Minuspixel Typ 2 (wie sehr führen Pixel außerhalb der Region zum Abzug) unterschiedlich bestrafen. Wie viele Pixel werden als Minuspixel zu der einen Region gezählt und wie viele zur anderen?
Dies geschieht nach folgender Heuristik: Bedeckt die Markierung nur eine Region, dann werden alle Punkte innerhalb der Markierung und außerhalb der Region als Minuspunkte Typ 2 der Region gezählt. In obigem Beispiel würden dann die Punkte A und B zur unteren linken Region gezählt, da die Markierung die andere Region nicht berührt. Wenn eine Markierung mehrere Regionen berührt, dann wird die Fläche der Markierung die außerhalb der Regionen liegt anteilig den verschiedenen Regionen zugeordnet. Der Anteil richtet sich dabei danach, wie viele Pixel der jeweiligen Region von der Markierung überdeckt werden. Es lassen sich natürlich Sonderfälle konstruieren, die hier zu relativ sinnfreien Auswertungen führen.

Links würde unsere Heuristik zu einer sinnvollen Bewertung gelangen, die rote Fläche würde entlang der weißen Linie aufgeteilt. Bei der mittleren Markierung hingegen, würde - obwohl davon auszugehen ist, dass hauptsächlich die Region rechts unten markiert werden sollte - die Hälfte der roten Fläche der anderen Region zugeordnet werden. Ändert man die Heuristik und teilt nach Relation von überdeckter Fläche zu Gesamtfläche auf, dann würde im rechten Beispiel ein viel zu großer Anteil der roten Fläche (nämlich die Hälfte, da beide Regionen komplett überdeckt sind) der kleinen Markierung rechts unten zugerechnet werden. Man könnte versuchen, die beiden Heuristiken gewichtet miteinander zu kombinieren, aber wie soll man das dann beim Feedback der Lernerin transparent machen?
Komplexere Aufteilungsalgorithmen, z.B. unter Berücksichtigung des Abstands zur nächsten Region, der Schwerpunkte der Regionen usw. verbieten sich leider, da die Berechnung hierbei zu komplex wären um noch in annehmbarer Zeit durchgeführt werden zu können und für das Beispiel oben links das vermutlich sinnvollste Ergebnis zu erreichen:

Selbst im Fall der einfacheren Heuristik muss darauf verzichtet werden, für jedes Pixel individuell zu ermitteln welcher Region es zugeordnet wird - etwa um anzeigen zu können, welche Minuspixel Typ 1 zu einer bestimmten Region gezählt werden. Das Berechnen der Anzahl der Pixel die jeweils den von der Markierung getroffenen Regionen zugeordnet werden muss reichen. Sonst müsste man dazu bei nur zwei betroffenen Regionen eine Trennlinie finden, die irgendwie sinnvoll zwischen den Regionen liegt. Die Richtung dieser Trennlinie zu berechnen ist aufwändig, und diese dann noch soweit hin und herzuschieben, dass sie die Fläche in genau dem richtigen Verhältnis teilt ist nicht-trivialer zusätzlicher Aufwand. Sind mehrere Regionen betroffen, dann müsste eine Zerlegung der Markierung ähnlich zu
Voronoi-Diagrammen berechnet werden - nur mit den Regionen statt Punkten als Zentren.
Bleibt noch die Frage, wie man mit Markierungen umgeht, die keine Region überdecken. Eigentlich müssten auch diese der bzw. in verschiedenen Anteilen den nähesten Region/en zugeordnet werden - da dies wegen des hohen Berechnungsaufwand aber ebenso wenig möglich ist, wie die Aufteilung einer Markierung die mehrere Regionen überdecken, wird diese Region einfach auf alle Regionen gemäß deren Größen aufgeteilt.
Video zur Auswertung (Regionen sind weiß, Markierungen gelb, beim Antippen einer Region werden die Pluspixel grün angezeigt, alle Minuspixel vom Typ 1
bzgl. der angetippten Region werden rot angezeigt, in das Ergebnis oben links fließen aber nur die tatsächlich dieser Region zugeordneten Minuspixel Typ 1. Die Minuspixel Typ 2 werden blau angezeigt. In der Demo sind keine Markierungen vorhanden, die keine Region überdecken.
Feedback
Das Feedback besteht aus zwei Komponenten: Einmal einem Text-Generator, der zur gewählten Region den zugehörigen Text erzeugt und zum anderen eine (schöne) Oberfläche. Eine spannende Frage ist, wo in der Oberfläche der Text angezeigt wird - das ist ja nicht trivial, da der Text den relevanten Teil der Oberfläche nicht verdecken darf. Da der Text-Generator relativ einfach umzusetzen ist (abgesehen von der nervigen Internationalisierung) soll hier nicht weiter darauf eingegangen werden - erwähnenswert ist hier dass bei der Generierung unterschieden wird zwischen Markierungsfragen bei denen nur eine Region zu markieren ist und solchen mit mehreren Regionen. Zudem erscheint bei nur einer Region die Erklärung sofort, bei mehreren Regionen erscheint ein Hinweis, dass man eine Region anwählen muss um die zugehörige Erklärung zu sehen.
Bei der Platzierung des Feedbacks wurde so vorgegangen, dass es 7 Stellen gibt, an denen der Kasten erscheinen kann: Oben/Mitte, Mitte/Links, Mitte/Mitte, Mitte/Rechts, Unten/Links, Unten/Mitte und Unten/Rechts. Oben/Links ist ggf. das Vergrößerungsfenster, Oben/Rechts ist der Schließen-Button.
Bei Öffnen des Fensters (bei mehreren Regionen) und Änderungen der Oberfläche (bei Verschieben wenn nur ein Ausschnitt des Bildes zu sehen ist) wird das die relevanten Objekte umschließende Rechteck berechnet und dann berechnet auf welcher Position das Feedback die wenigste Überschneidung hat.
Ein Problem das dabei auftritt ist, dass zur Berechnung der Überschneidung zwischen Feedback-Fenster und relevantem Rechteck nicht das Feedback-Fenster bewegt werden kann, das würde man als Flackern wahrnehmen. Stattdessen wird: In die Feedback-Box der richtige Text eingesetzt (so dass die Feedback-Box die richtige Größe hat), ein unsichtbares Element mit der genau gleichen Größe erzeugt, dieses an alle möglichen Positionen gesetzt und die Überschneidung berechnet, die optimale Position ausgewählt, das unsichtbare Element wieder entfernt und abschließend die Feedback-Box ggf. umpositioniert. Die optimale Position ist dabei die, bei der die Überschneidung am minimal ist und falls mehrere Positionen hier gleich sind, dann wird die bevorzugt, bei der das umgebende Rechteck um das relevante Rechteck der Markierungen und Regionen und um das Feedback-Fenster minimal ist.
Zunächst wurde versucht, die Positionierung über eine CSS-Klasse des umgebenden HTML-Elements zu realisieren, doch leider war dies zu langsam: Wurde direkt danach die Überschneidung ausgerechnet, dann war die Box noch nicht umgesetzt und der alte Wert als neuer Wert berechnet. Man hätte hier mit MutationObservern usw. arbeiten müssen, was zu aufwändig war. Danach wurde die Position über eine CSS-Klasse des Elements selbst verändert und dies funktioniert.
Video zum Feedback
Um unnötiges Springen (wie im Video zu sehen) zu verhindern wird zusätzlich bei Verschieben des Ausschnitts gemerkt, an welcher Position das Feedback zuletzt platziert war und nur wenn das umgebende Rechteck das Feedback berührt wird die Position geändert.
[TBD: Upload, Failures]
Änderungen
Nach ersten Tests ist aufgefallen, dass die zuwenig markierte Fläche hier doppelt als falsch gezählt wird: Einmal weil nur die überdeckte Fläche als Plus-Prozentpunkte gewertet wird und danach wird nochmal die fehlende Fläche als Minus-Prozentpunkte abgezogen. Aus diesem Grund wurde das Einlesen und der Player so verändert, dass bei fehlendem Wert der Default-Wert 0 gesetzt wird, der bedeutet dass die fehlende Fläche nicht mehr doppelt abgezogen wird.
Momentanes Endprodukt
Kompletter Fall mit Grafik-Eingabe-Fragen und Grafik-Markierungs-Fragen